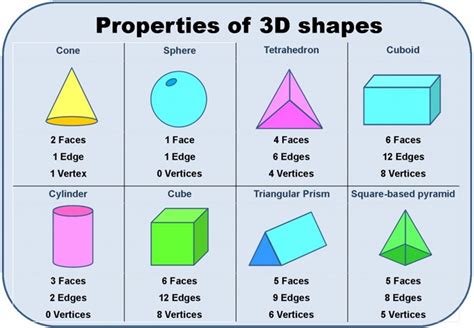
Military
3 Edges On Cone
Introduction to Cones and Their Properties
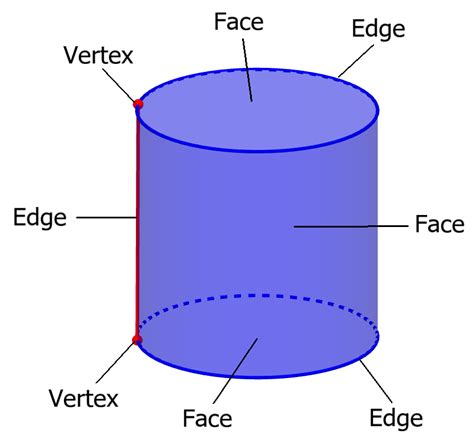
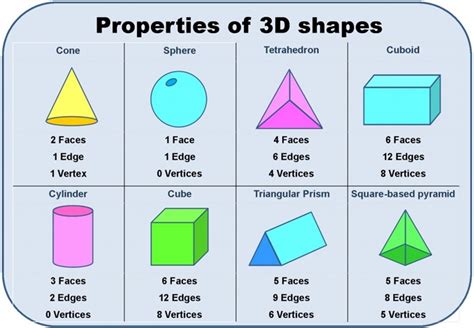
A cone is a three-dimensional geometric shape that typically has a circular base and tapers to a point, known as the apex or vertex. Cones are common in various aspects of life, from architecture to nature, and their properties make them interesting subjects for study in geometry and mathematics. One of the unique features of a cone is its edges. When considering the edges of a cone, it’s essential to understand the basic structure of a cone, which includes its base, lateral surface, and the apex.
Understanding Edges on a Cone
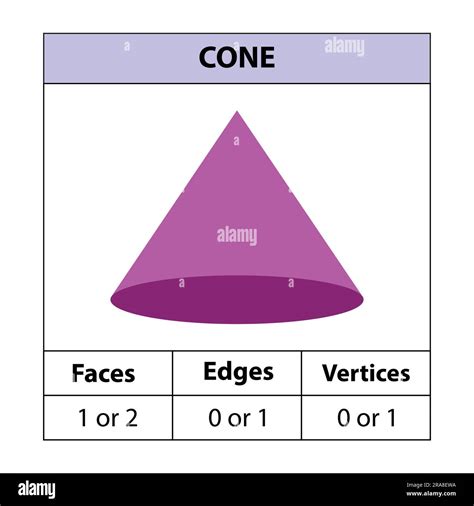
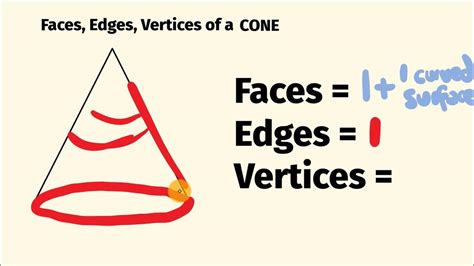
In the context of a cone, an edge refers to the boundary or the rim of the cone’s base and the line that connects the base to the apex. However, when counting the edges of a cone, we often consider the number of edges that form the shape’s outline. For a standard cone, there is one edge at the base (the circular edge of the base) and one edge that theoretically could be considered as the line connecting the apex to the base, but in practical geometric terms, a cone is said to have one edge when considering its one-dimensional boundary - the edge of the base.
Clarification on the Number of Edges
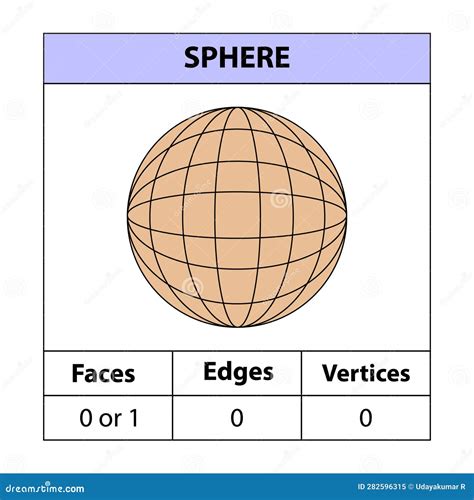
The confusion about the number of edges on a cone might stem from how one defines an edge in the context of three-dimensional geometry. For polyhedra (three-dimensional solids with flat faces), edges are the lines where two faces meet. A cone, however, does not have flat faces like polyhedra but rather a continuous curved surface. Therefore, when discussing cones in terms of edges, it’s more about understanding the conceptual difference between a cone and polyhedral shapes.
Properties of Cones
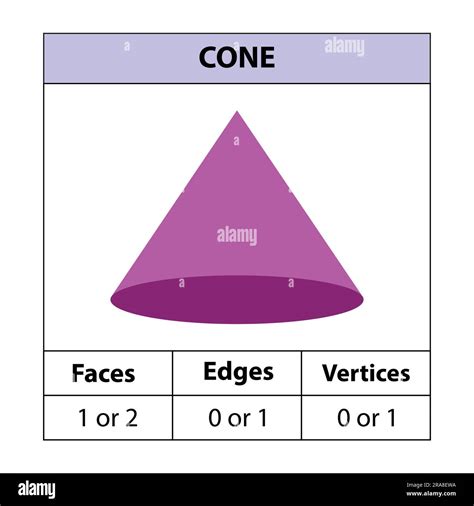
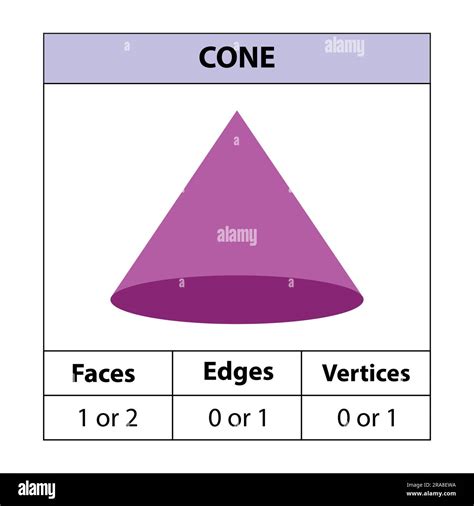
Cones have several interesting properties: - Circular Base: The base of a cone is always a circle. - Apex: The point at which the cone tapers to is called the apex. - Lateral Surface: The surface of the cone, excluding the base, is called the lateral surface. - Height: The distance from the apex to the base is the height of the cone. - Slant Height: The distance from the apex to any point on the edge of the base is the slant height.
📝 Note: When discussing the edges of a cone in geometric terms, it's crucial to differentiate between the concept of edges in polyhedra and the unique, continuous surface of a cone.
Applications and Examples of Cones

Cones are found in various aspects of life, from the design of roofs and hats to the shapes of certain types of flowers and volcanoes. Their unique geometry makes them efficient for containing or directing materials (like in the case of funnels) and for structural purposes due to their strength and stability.
| Property | Description |
|---|---|
| Base | Circular shape |
| Apex | Point where the cone tapers |
| Lateral Surface | Continuous curved surface excluding the base |
Conclusion and Final Thoughts
In summary, when discussing the edges of a cone, it’s essential to understand the geometric definitions and properties that distinguish a cone from other three-dimensional shapes. The concept of edges on a cone is nuanced and requires an understanding of its unique geometry. Whether in nature, architecture, or design, cones play a significant role, and their properties make them an interesting subject for study and application.
What is the basic structure of a cone?
+
A cone consists of a circular base, a lateral surface, and an apex.
How many edges does a cone have?
+
In geometric terms, a cone is considered to have one edge, which is the edge of its circular base.
What are some common applications of cones?
+
Cones are used in various applications, including architecture, design, and nature, due to their unique properties and strength.
Related Terms:
- Cylinder faces edges vertices
- cone faces edges vertices
- Sphere faces edges vertices
- Cone Have edge
- Edges of cube
- Cone is



